
“Binary search is one of the most powerful ideas in algorithm design.” — Steven S. Skiena, The Algorithm Design Manual
This piece is about the profound importance of a relatively simple algorithm, binary search. It’s a story of how binary search (and more generally, functions with logarithmic time complexity) can performantly search extremely large datasets. The implementation code is in Swift, although the principles generalize across languages. Say you were handed a phonebook of Gotham (hypothetical population one million) and asked to find the name Ron Swanson. How would you do it?
The Strategy
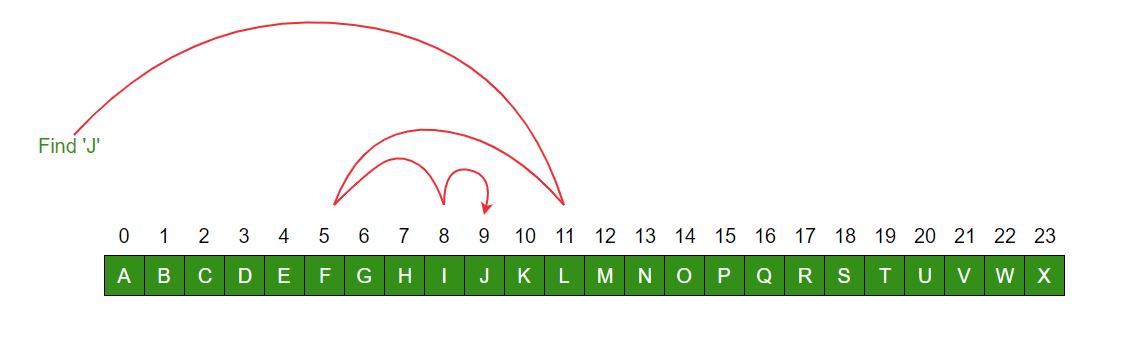
The extremely naive approach opens on page one, scans every name on the page for Ron Swanson, and continues to page two and beyond until found (or not). This is, of course, very, very slow, requiring the reading of an average 500,000 names before finding a random target. This is pretty silly and (hopefully) not at all like how a rational human would approach the problem. This is because a rational human intuitively knows something about the phonebook dataset: It’s presorted. This characteristic can be exploited to massively speed up search. For starters, they could use the published index at the beginning of the phonebook to start their search on the first page of last names that begin with S. In fact, this is probably a component of the ideal solution for this particular problem. However, a better intra-page strategy than reading names linearly from the top is still needed. Luckily, our hyper-rational human knows about binary search and its applicability to this problem.
So our hyper-rational human opens the phonebook exactly midway to the name John Michaels. Since Ron Swanson comes after John Michaels, she then knows the target must exist in the second half of the phonebook (50% of the search area eliminated by a single read!). She then repeats the process of picking the middle of the now smaller search area and evaluating it against the target. Each step reduces the overall search area by 50%. This is so efficient that any name in the million-person phone book can be found in only 20 reads. This isn’t a magic number. In fact, some of you may immediately recognize the nature of the relationship between it and the size of our hypothetical dataset (one million).
log2(1,000,000) ~= 20
We have discovered a binary logarithmic function. Its main calling card: a problem space that halves at every step. Furthermore, we have seen what an incredible speedup this can provide on a large dataset. Assuming reading a name takes a human 100ms, our super naive human would have spent 14 hours reading names alone. Our champion of enlightened searching need spend only two seconds reading names.
the larger the dataset, the more pronounced the time savings. source: https://www.quora.com/Which-one-is-better-binary-search-or-linear-search It turns out this search strategy can be used to search any type of sorted, bounded data that allows random access. The 25,000x speedup of our contrived example may seem unrealistic. After all, the naive case seems hopelessly naive (who would really search a phonebook by reading names one at a time from the beginning?). But this is actually quite common (a full table scan in a database is one such example). Furthermore, this level of speed improvement is a characteristic of switching from a linear time complexity algorithm (e.g., a full table scan) to one with logarithmic time complexity (e.g., a database query against an indexed column). Astute readers may note we have not fully optimized the speed of our name-finding algorithm. By utilizing the phonebook’s index (and assuming a normal character distribution of last names) to define our initial search space, we can improve our algorithm to require a maximum of log2(1,000,000 / 26) ~= 16 reads to find any given name in this specific problem.
How Is It Implemented?
Generic binary search can be implemented either iteratively or recursively on any static sorted collection that allows random access. Implementations are generally simple and concise. Interestingly, the recursive implementation benchmarked much faster than the iterative one in Swift. (These benchmarks are available at the end of the article.)
iterative
func binarySearchIterative<T: Comparable, E: RandomAccessCollection>(_ xs: E, target: T) -> E.Index? where E.Element == T {
// Start with two indexes, one at the beginning
var startIndex = xs.startIndex;
// And one at the end
var endIndex = xs.index(before: xs.endIndex);
// We are done when are our indexes converge
while startIndex < endIndex {
// Find the midpoint between our current range
let midPoint = xs.index(startIndex, offsetBy: xs.distance(from: startIndex, to: endIndex) / 2);
let midValue = xs[midPoint];
// Evaluate the middle value against our target value
if ( target < midValue ) {
// If the target is less than our middle value,we can narrow the search space to
// [start, mid]
endIndex = midPoint
} else if ( target > midValue ) {
// If the target is greater than our middle value,we can narrow the search space to
// [mid, end]
startIndex = min(midPoint, xs.index(after: startIndex))
} else {
// If the target is equal, we've found it
return midPoint;
}
}
// We did not find a match
return nil;
}
recursive
func binarySearchRecursive<T: Comparable, E: RandomAccessCollection>(_ xs: E, target: T, start _start: E.Index? = nil, end _end: E.Index? = nil) -> E.Index? where E.Element == T {
// Base cases
guard !xs.isEmpty else { return nil; }
guard xs.count > 1 else {
return xs[xs.startIndex] == target ? xs.startIndex : nil
}
// Start with two indexes, optionally supplied
let startIndex = _start ?? xs.startIndex;
let endIndex = _end ?? xs.endIndex;
// Calculate the middle index
let midPoint = xs.index(startIndex, offsetBy: xs.distance(from: startIndex, to: endIndex) / 2);
let midValue = xs[midPoint];
// Compare middle value to target value
if ( target < midValue ) {
// recursively search the new search space of: [start, mid]
return binarySearchRecursive(xs, target: target, start: startIndex, end: midPoint);
} else if ( target > midValue ) {
// recursively search the new search space of [mid, end]
return binarySearchRecursive(xs, target: target, start: midPoint, end: endIndex)
} else {
// If the target is equal, we've found it
return midPoint;
}
}
Speed

let ARRAY_SIZE = 10000000; // 10 million
class BinarySearchTests: XCTestCase {
let testPerformanceArray: [Int] = makeSortedArray(ARRAY_SIZE);
var randomTarget = Int.random(in: 0..<ARRAY_SIZE));
func testIterativePerformance() {
self.measure {
let _ = binarySearchIterative(testPerformanceArray, target: randomTarget)
}
}
func testRecursivePerformance() {
self.measure {
let _ = binarySearchRecursive(testPerformanceArray, target: randomTarget)
}
}
func testNaiveFind() {
self.measure {
let _ = testPerformanceArray.firstIndex(of: randomTarget)
}
}
}
test code
I could have guessed testNaiveFind’s use of firstIndex (and ignorance as to whether the supplied array is sorted) doomed it to linear performance, but I’m stumped as to the order of magnitude difference between the iterative and recursive binary search functions. Any readers have an explanation?